
こんにちはー、ニアです。
私は1月31日にpaiza主催の「【ITエンジニアを目指す2017卒学生対象!!】 paizaでpizzaを食べながらもぐもぐ就活勉強会」に参加します。
今回はそのイベントの事前課題「パイザオンラインハッカソン・Lite 」を解いて、動的計画法の復習をしました。
使用した言語はC#です。
1. 事前課題(POH Lite)の概要
標準入力からプロジェクトに必要な人員数と下請け会社の人員数・発注費用を読み込み、必要な人員数を満たす最も発注費用が安い組み合わせの時の合計金額を出力します。
// フォーマット
m
n
q1 r1
q2 r2
…
qn rn
// 凡例
m : プロジェクト人数(1~200000)
n : 下請け会社の数(1~50)
q1..qn : 各下請け会社の人員数(1~10000)
r1..rn : 各下請け会社の発注費用(1~5000000)
// 入力例
60
3
40 4300
30 2300
20 2400
// 実行結果
6600
2. 動的計画法の「ど」の字をまだ知らなかった当時の私が解いたプログラム
実はこの問題は2回チャレンジしています。最初にチャレンジした頃は動的計画法を知りませんでした。
下請け会社が最大50社ということで、64ビット整数型を利用して1から2のm乗までの整数をビットの列として表現します。各下請け会社の人員数と発注費用を格納する配列を作り、先ほどの64ビット整数の各ビットを調べて、1である位置をインデックスとして利用し、人員数と発注費用の合計金額を求めます。
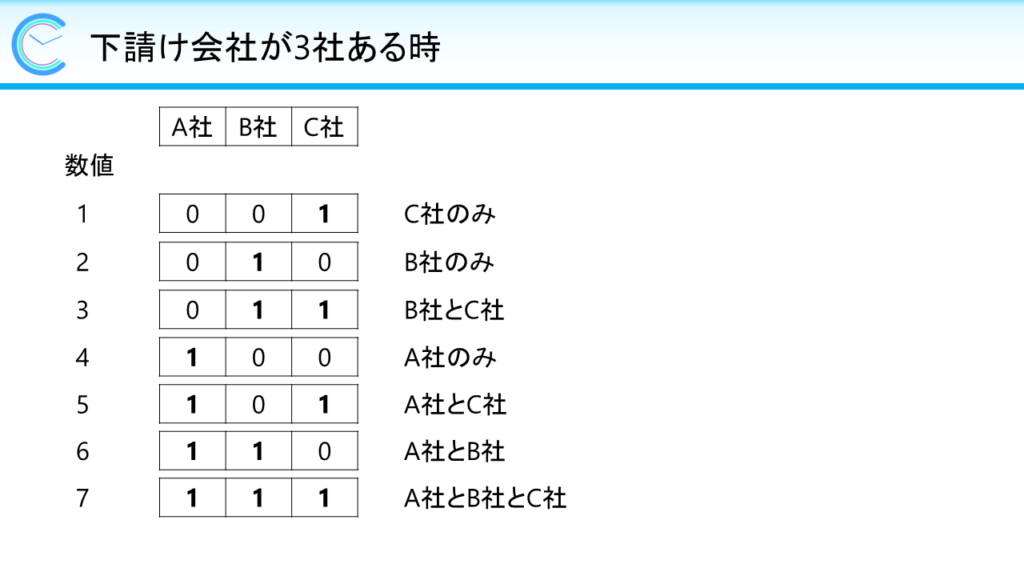
また、内側のfor文の繰り返し条件に、
using System;
class Program {
struct Comp {
public int Mem; // 下請け会社の人員数
public int Cost; // 下請け会社への発注費用
}
static void Main( string[] args ) {
// reqProjItem : プロジェクトに必要な人数
int reqProjMem = int.Parse( Console.ReadLine() );
// numComp : 下請け会社数
int numComp = int.Parse( Console.ReadLine() );
// 各下請け会社の人員数と発注費用のリスト
Comp[] compMemCost = new Comp[numComp];
// ans : 発注費用の最小値を格納します。
int ans = 5000000 * numComp;
// 各下請け会社の人員数と発注費用を読み込みます。
string[] s;
for( int i = 0; i < numComp; i++ ) {
s = Console.ReadLine().Split( ' ' );
compMemCost[i].Mem = int.Parse( s[0] );
compMemCost[i].Cost = int.Parse( s[1] );
}
// 組み合わせ数の最大( 2のnumComp乗 )を求めます。
long bmax = ( long )Math.Pow( 2, numComp );
// 1から2のnumComp乗まで繰り返します。
for( long b = 1; b < bmax; b++ ) {
long bi = b;
Comp ci = new Comp();
// biをビットの列として表した時、ビットが1である位置を
// インデックスとして利用し、人員数と発注費用の合計金額を求めます。
for( int i = 0; i < numComp && bi > 0 && ci.Mem < reqProjMem && ans > ci.Cost; i++, bi >>= 1 ) {
if( ( bi & 1 ) != 0 ) {
ci.Mem += compMemCost[i].Mem;
ci.Cost += compMemCost[i].Cost;
}
}
// プロジェクトに必要な人数以上かつ、発注費用がより安い時、合計金額を更新します。
if( ci.Mem >= reqProjMem && ans > ci.Cost )
ans = ci.Cost;
}
// 合計金額を出力します。
Console.WriteLine( ans );
}
}このプログラムを実行したところ、7つテストケースの内、テストケース5までが通りました。しかし、テストケース6でタイムオーバーしました。
テストケース1:success 0.03秒
テストケース2:success 0.03秒
テストケース3:success 0.03秒
テストケース4:success 0.04秒
テストケース5:success 0.05秒
テストケース6:invalid (タイムオーバー)
テストケース7:invalid (スキップ)Score : 71 / 100 Rank : A
下請け会社が最大の50社の時、bmaxの値は2の50乗すなわち1000兆以上ものパターンを調査していることになります。
3. 動的計画法で解いてみよう
そこで、人員数と発注費用の合計を格納するリストを作成し、新たに追加する要素と今まで格納されている各要素との人員数と発注費用の合計を求めて、それぞれリストに追加します。
下請け会社が3社(A社、B社、C社)の時、
- A社の人員数と発注費用をリストに追加します。
- B社の人員数と発注費用をリストに追加します。
- A社とB社の人員数及び発注費用の合計を求めて、リストに追加します。
- C社の人員数と発注費用をリストに追加します。
- A社とC社、B社とC社の人員数及び発注費用の合計を求めて、それぞれリストに追加します。
- A社とB社とC社の人員数及び発注費用の合計を求めて、リストに追加します。
手順6において、A社とB社の人員数及び発注費用の合計はリストに追加済みなので、それを利用して求めていきます。
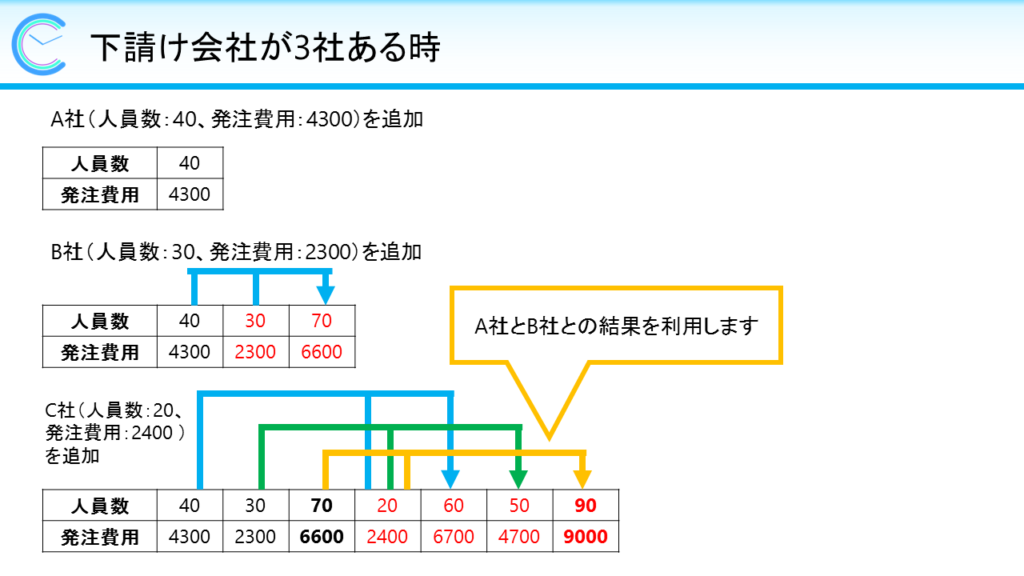
このように、既知の計算結果を利用して求めていきます。
また、求める値は最も安い発注費用なので、同じ人員数の時には発注費用を安い方に更新していくことで、リストの要素数を節約し、計算回数を減らすことができます。
2.1. C#でコーディング
それでは、C#でコードを書いてみましょう。.NET FrameworkのDictionaryクラスを利用して、人員数をキーに求めた発注費用の合計を追加します。
// 下請け会社を組み合わせた時の人員数と発注費用のリスト
Dictionary<int, int> compMemCost = new Dictionary<int, int>();foreach文でリスト列挙する場合、あらかじめそのリストの複製を作り、それを列挙していきます。
// 現在のリストを複製し、列挙します。
foreach( var item in compMemCost.ToList() ) {
// ...
}Dictionaryクラスのインデクサーで値をセットする時、指定したキーがリストになければ、新たなキーと値のペアとして追加されます。
Dictionary<int, int> compMemCost = new Dictionary<int, int>();
compMemCost.Add( 1, 50 );
// キー「1」はリストに存在するので、関連付けれた値を100にセットします。
compMemCost[1] = 100;
// キー「2」はリストに存在しないので、その2をキーにと80とのペアを新たに追加します。
compMemCost[2] = 80;人員数と発注費用のリストができたら、LINQのWhereメソッドでプロジェクトに必要な人数を満たす要素を抽出し、Minメソッドで発注費用の合計の最小値を求めます。
compMemCost.Where( _ => _.Key >= reqProjMem ).Min( _ => _.Value )完成したプログラムを下に示します。
using System;
using System.Collections.Generic;
using System.Linq;
class Program {
static void Main( string[] args ) {
// reqProjItem : プロジェクトに必要な人員数
int reqProjMem = int.Parse( Console.ReadLine() );
// numComp : 下請け会社数
int numComp = int.Parse( Console.ReadLine() );
// 下請け会社を組み合わせた時の人員数と発注費用のリスト
Dictionary<int, int> compMemCost = new Dictionary<int, int>();
// 新たに読み込む各下請け会社のみの要素を追加するために、空の人員数と発注費用を追加します。
compMemCost.Add( 0, 0 );
// 下請け会社のの数だけ繰り返します。
for( int i = 0; i < numComp; i++ ) {
// mem : i社の下請け会社のの人員数
// cost : i社の下請け会社のへの発注費用
string[] s = Console.ReadLine().Split( ' ' );
int mem = int.Parse( s[0] ),
cost = int.Parse( s[1] );
// 現在のリストを複製し、列挙します。
foreach( var item in compMemCost.ToList() ) {
// men1 : リストに登録済みの人員数とi社の人員数の和
// cost1 : リストに登録済みの発注費用とi社の発注費用の和
int mem1 = mem + item.Key;
int cost1 = cost + item.Value;
// men1の時の発注費用データが未登録 or 登録済みの発注費用データよりcost1が小さい時、リストに追加 or 設定します。
// ※条件OR演算子のショートサーキット評価を利用しています。
if( !compMemCost.ContainsKey( mem1 ) || compMemCost[mem1] > cost1 ) {
// Dictionaryクラスのインデクサーのsetプロパティで、キーが存在する時はそれに関連付けられた値を設定し、
// そうでない時は、mem1をキーににcost1とのペアを新規に追加します。
compMemCost[mem1] = cost1;
}
}
}
// LINQを使って、プロジェクトに必要な人数以上の持つ要素を抽出し、その中の発注費用の最小値を出力します。
Console.WriteLine(
compMemCost.Where( _ => _.Key >= reqProjMem )
.Min( _ => _.Value )
);
}
}2.2. 条件文のショートサーキット評価でコードがスリムに
ところで、if文の条件文が以下のような構成にしているのは、条件OR演算子「||」より前の条件式がtrueの時に「||」以降の条件式の評価がスキップされる仕組み(ショートサーキット評価)を利用しているからです。
// men1の時の発注費用データが未登録 or 登録済みの発注費用データよりcost1が小さい時、リストに追加 or 設定します。
// ※条件OR演算子のショートサーキット評価を利用しています。
if( !compMemCost.ContainsKey( mem1 ) || compMemCost[mem1] > cost1 ) {
// ...
}Dictionaryクラスのインデクサーで値を取得する時、指定したキーがリストに存在しない場合、例外(KeyNotFoundException)がスローされます。そこで条件OR演算子を使用して、
「!compMemCost.ContainsKey( mem1 )」、「compMemCost[mem1] > cost1」の順
に並べ、指定したキーがリストに存在しない時(「!compMemCost.ContainsKey( mem1 )」の結果がtrue)は、「compMemCost[mem1] > cost1」の評価をスキップするようにします。
こうすることで、リストに存在しないキーを指定して値を取得してしまうというエラーを回避することができます。

このプログラムを実行したところ、7つテストケースの内、すべて通りました。
テストケース1:success 0.04秒
テストケース2:success 0.04秒
テストケース3:success 0.04秒
テストケース4:success 0.04秒
テストケース5:success 0.04秒
テストケース6:success 0.12秒
テストケース7:success 0.38秒Score : 100 / 100 Rank : S
2.3. さらに効率のよいコードにする
プロジェクトに必要な人員数を満たす最安の発注費用の合計をLINQで求める代わりに、変数1つに「下請け会社をすべて利用する時の発注費用の合計」で初期化して、安い値にどんどん更新していく方法でやってみましょう。
まず、各社の下請け会社の人員数と発注費用を格納する構造体を作成し、
// 各社の下請け会社の人員数と発注費用
struct MemCost {
// Mem : 各社の下請け会社のの人員数
public int Mem;
// Cost : 各社の下請け会社のへの発注費用
public int Cost;
}標準入力からの読み込みます。そのついでに下請け会社をすべて利用する時の発注費用の合計を求めます。
// minTotalCost : 発注費用の合計の最小値
int minTotalCost = 0;
// memCosts : 各下請け会社の人員数と発注費用の配列
MemCost[] memCosts = new MemCost[numComp];
// 各下請け会社の人員数と発注費用を読み込みます。
for( int i = 0; i < numComp; i++ ) {
string[] s = Console.ReadLine().Split( ' ' );
memCosts[i].Mem = int.Parse( s[0] );
memCosts[i].Cost = int.Parse( s[1] );
// 下請け会社をすべて利用する時の発注費用の合計を求めます。
minTotalCost += memCosts[i].Cost;
}
あとはPOH3-Lite2.csと同じように、Dictionaryクラスで下請け会社を組み合わせた時のプロジェクトの人数と発注費用のリストを作るのですが、
// 現在のリストを複製し、列挙します。
foreach( var item in compMemCost.ToList() ) {
// men1 : 現在の要素の人員数と既知の人員数の和
// cost1 : 現在の要素の発注費用と既知の人員数に対する発注費用の和
int mem1 = memCost.Mem + item.Key;
int cost1 = memCost.Cost + item.Value;
// mem1がプロジェクトに必要な人数より少ない時
if( mem1 < reqProjMem ) {
// men1に対する発注費用の合計が未登録 or 登録済みの発注費用の合計よりcost1が小さい時、リストに追加 or その要素を更新します。
// ※条件OR演算子のショートサーキット評価を利用しています。
if( !compMemCost.ContainsKey( mem1 ) || compMemCost[mem1] > cost1 ) {
// Dictionaryクラスのインデクサーのsetプロパティで、キーが存在する時はそれに関連付けられた値を設定し、
// そうでない時は、mem1をキーににcost1とのペアを新規に追加します。
compMemCost[mem1] = cost1;
}
}
// mem1がプロジェクトに必要な人数を満たしているならば、
// cost1が今まで求めた発注費用の合計の最小値より小さい時、
// その最小値を更新します。
else if( minTotalCost > cost1 ) {
minTotalCost = cost1;
}
}現在の要素の人員数(memCost.Mem)と既知の人員数(item.Key)の和(mem1)が、プロジェクトに必要な人員数を満たしているかどうかで条件分岐を行います。
- 満たしている時、今まで求めた発注費用の合計の最小値より小さい時、その最小値を更新
- 満たしていない時、 men1に対する発注費用の合計が未登録 or 登録済みの発注費用の合計より、現在の要素の発注費用(memCost.Cost)と既知の人員数に対する発注費用の合計(item.Value)の和(cost1)が小さい時、mem1とcost1を新たなペアとしてリストに追加 or mem1に対する値を更新
なぜなら、memCost.Costがすでにプロジェクトに必要な人員数を満たしている場合、既知の人員数と組合せる必要がなく、またmem1がプロジェクトに必要な人員数を満たしている場合、以降の要素の人員数と組合せる必要がないからです。

こうすることで、リストの要素数をさらに節約することができます。
using System;
using System.Collections.Generic;
using System.Linq;
class Program {
// 各社の下請け会社の人員数と発注費用
struct MemCost {
// Mem : 各社の下請け会社のの人員数
public int Mem;
// Cost : 各社の下請け会社のへの発注費用
public int Cost;
}
static void Main( string[] args ) {
// reqProjItem : プロジェクトに必要な人員数
int reqProjMem = int.Parse( Console.ReadLine() );
// numComp : 下請け会社数
int numComp = int.Parse( Console.ReadLine() );
// minTotalCost : 発注費用の合計の最小値
int minTotalCost = 0;
// memCosts : 各下請け会社の人員数と発注費用の配列
MemCost[] memCosts = new MemCost[numComp];
// 各下請け会社の人員数と発注費用を読み込みます。
for( int i = 0; i < numComp; i++ ) {
string[] s = Console.ReadLine().Split( ' ' );
memCosts[i].Mem = int.Parse( s[0] );
memCosts[i].Cost = int.Parse( s[1] );
// 下請け会社をすべて利用する時の発注費用の合計を求めます。
minTotalCost += memCosts[i].Cost;
}
// 人員数と発注費用の合計との既知のペアのリスト
Dictionary<int, int> compMemCost = new Dictionary<int, int>();
// 新たに読み込む各下請け会社のみの要素用に、空の人員数と発注費用を追加します。
compMemCost.Add( 0, 0 );
// 各下請け会社の人員数と発注費用を列挙します。
foreach( var memCost in memCosts ) {
// 現在のリストを複製し、列挙します。
foreach( var item in compMemCost.ToList() ) {
// men1 : 現在の要素の人員数と既知の人員数の和
// cost1 : 現在の要素の発注費用と既知の人員数に対する発注費用の和
int mem1 = memCost.Mem + item.Key;
int cost1 = memCost.Cost + item.Value;
// mem1がプロジェクトに必要な人数より少ない時
if( mem1 < reqProjMem ) {
// men1に対する発注費用の合計が未登録 or 登録済みの発注費用の合計よりcost1が小さい時、リストに追加 or その要素を更新します。
// ※条件OR演算子のショートサーキット評価を利用しています。
if( !compMemCost.ContainsKey( mem1 ) || compMemCost[mem1] > cost1 ) {
// Dictionaryクラスのインデクサーのsetプロパティで、キーが存在する時はそれに関連付けられた値を設定し、
// そうでない時は、mem1をキーににcost1とのペアを新規に追加します。
compMemCost[mem1] = cost1;
}
}
// mem1がプロジェクトに必要な人数を満たしているならば、
// cost1が今まで求めた発注費用の合計の最小値より小さい時、
// その最小値を更新します。
else if( minTotalCost > cost1 ) {
minTotalCost = cost1;
}
}
}
// 発注費用の合計の最小値を出力します。
Console.WriteLine( minTotalCost );
}
}このプログラムを実行したところ、7つテストケースの内、すべて通りました。POH3-Lite2.csより、テストケース6で0.04秒、テストケース7で0.02秒速くなりました。
テストケース1:success 0.04秒
テストケース2:success 0.04秒
テストケース3:success 0.04秒
テストケース4:success 0.04秒
テストケース5:success 0.04秒
テストケース6:success 0.08秒
テストケース7:success 0.36秒Score : 100 / 100 Rank : S
4. パターンの数はいくつあるの?
今回のストーリーに登場する火村氏が書いたコードを見てみましょう。
//霧島氏、これが私の書いたコードですぞ。ほぼ完璧なので、後は頼みましたぞ!
using System;
using System.IO;
using System.Text;
using System.Linq;
using System.Collections;
using System.Diagnostics;
using System.Collections.Generic;
public class ClassName
{
public static void Main()
{
int m = int.Parse(Console.ReadLine());
int n = int.Parse(Console.ReadLine());
//一社だけの場合
if (n == 1)
{
string line = Console.ReadLine();
string[] tmp = line.Split(' ');
int ningetsu_A = int.Parse(tmp[0]);
int cost_A = int.Parse(tmp[1]);
int total_cost = cost_A;
int total_ningetsu = ningetsu_A;
if (m <= total_ningetsu)
{
Console.WriteLine(total_cost);
}
}
//2社あるパターン
//A社を使う、B社を使う
//A社を使う
//B社を使う
if (n == 2)
{
//入力処理
string[] tmp = Console.ReadLine().Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
int ningetsu_A = int.Parse(tmp[0]);
int cost_A = int.Parse(tmp[1]);
tmp = Console.ReadLine().Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
int ningetsu_B = int.Parse(tmp[0]);
int cost_B = int.Parse(tmp[1]);
//ここまで
//A社を使う、B社を使う 一番高いコストに絶対なるので答えを更新
int total_cost = cost_A + cost_B;
int total_ningetsu = ningetsu_A + ningetsu_B;
int ans = total_cost;
//A社を使う
total_cost = cost_A;
total_ningetsu = ningetsu_A;
if (m <= total_ningetsu && ans > total_cost)//人月数を満たして、コストが低ければ
{
ans = total_cost; //答えを更新
}
//B社を使う
total_cost = cost_B;
total_ningetsu = ningetsu_B;
if (m <= total_ningetsu && ans > total_cost) //人月数を満たして、コストが低ければ
{
ans = total_cost; //答えを更新
}
Console.WriteLine(ans);
}
//3社あるパターン
//A社を使う、B社を使う、C社を使う
//A社を使う、B社を使う
//A社を使う、C社を使う
//A社を使う
//B社を使う、C社を使う
//B社を使う
//C社を使う
if (n == 3)
{
//入力処理
string[] tmp = Console.ReadLine().Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
int ningetsu_A = int.Parse(tmp[0]);
int cost_A = int.Parse(tmp[1]);
tmp = Console.ReadLine().Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
int ningetsu_B = int.Parse(tmp[0]);
int cost_B = int.Parse(tmp[1]);
tmp = Console.ReadLine().Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
int ningetsu_C = int.Parse(tmp[0]);
int cost_C = int.Parse(tmp[1]);
//ここまで
//A社を使う、B社を使う、C社を使う 一番高いコストに絶対なるので答えを更新
int total_cost = cost_A + cost_B + cost_C;
int total_ningetsu = ningetsu_A + ningetsu_B + ningetsu_C;
int ans = total_cost;
//A社を使う、B社を使う
total_cost = cost_A + cost_B;
total_ningetsu = ningetsu_A + ningetsu_B;
if (m <= total_ningetsu && ans > total_cost) //人月数を満たして、コストが低ければ
{
ans = total_cost;//答えを更新
}
//A社を使う、C社を使う
total_cost = cost_A + cost_C;
total_ningetsu = ningetsu_A + ningetsu_C;
if (m <= total_ningetsu && ans > total_cost) //人月数を満たして、コストが低ければ
{
ans = total_cost;//答えを更新
}
//A社を使う
total_cost = cost_A;
total_ningetsu = ningetsu_A;
if (m <= total_ningetsu && ans > total_cost) //人月数を満たして、コストが低ければ
{
ans = total_cost;//答えを更新
}
//B社を使う、C社を使う
total_cost = cost_B + cost_C;
total_ningetsu = ningetsu_B + ningetsu_C;
if (m <= total_ningetsu && ans > total_cost) //人月数を満たして、コストが低ければ
{
ans = total_cost;//答えを更新
}
//B社を使う
total_cost = cost_B;
total_ningetsu = ningetsu_B;
if (m <= total_ningetsu && ans > total_cost) //人月数を満たして、コストが低ければ
{
ans = total_cost;//答えを更新
}
//C社を使う
total_cost = cost_C;
total_ningetsu = ningetsu_C;
if (m <= total_ningetsu && ans > total_cost) //人月数を満たして、コストが低ければ
{
ans = total_cost;//答えを更新
}
Console.WriteLine(ans);
}
// ここまで作るのに2年11ヶ月かかってしまった。もしかして効率悪いのか?
// 4社あるパターン
// 誰かが作る…
// 5社あるパターン
// 誰かが作る…
// 6社あるパターン
// 誰かが作る…
// 7社あるパターン
// 誰かが作る…
// 8社あるパターン
// 誰かが作る…
// 9社あるパターン
// 誰かが作る…
// 10社あるパターン
// 誰かが作る…
// 11社あるパターン
// 誰かが作る…
// 12社あるパターン
// 誰かが作る…
// 13社あるパターン
// 誰かが作る…
// 14社あるパターン
// 誰かが作る…
// 15社あるパターン
// 誰かが作る…
// 16社あるパターン
// 誰かが作る…
// 17社あるパターン
// 誰かが作る…
// 18社あるパターン
// 誰かが作る…
// 19社あるパターン
// 誰かが作る…
// 20社あるパターン
// 誰かが作る…
// 21社あるパターン
// 誰かが作る…
// 22社あるパターン
// 誰かが作る…
// 23社あるパターン
// 誰かが作る…
// 24社あるパターン
// 誰かが作る…
// 25社あるパターン
// 誰かが作る…
// ・・・
// 50社あるパターン
// 誰かが作る…
}
}https://paiza.jp/poh/kirishima の「火村氏のヒント」より
下請け会社がm社ある時のパターンの数は、以下の画像の式に示すように、組み合わせ「mC1」から「mCm」までの総和(※2のm乗-1と等価)です。

using System;
using System.Numerics;
class Program {
// 組み合わせ nCr を求めます。
// ※巨大な数値を格納するので、BigIntegerを利用します。
static BigInteger Combinate( int n, int r ) {
BigInteger ans = 1;
// 順列 nPr を求めます。
for( int i = n; i > n - r; i-- ) {
ans *= i;
}
// rの階乗分だけ、割ります。
for( int i = 2; i <= r; i++ ) {
ans /= i;
}
return ans;
}
// nのk乗を求めます。
// ※巨大な数値を格納するので、BigIntegerを利用します。
static BigInteger Pow( int n, int k ) {
BigInteger ans = 1;
while( k-- > 0 ) {
ans *= n;
}
return ans;
}
static void Main( string[] args ) {
int n = 50;
// 50C1~50C50までの総和を求めます。
BigInteger ans = 0;
for( int i = 1; i <= n; i++ ) {
BigInteger t = Combinate( n, i );
ans += t;
Console.WriteLine( $"{n}C{i} = {t} : Total = {ans}" );
}
Console.WriteLine();
// 50C1~50C50までの総和と等価な、2^50 - 1を求めます。
Console.WriteLine( $"2^{n} - 1 = {Pow( 2, n ) - 1}" );
}
}つまり、下請け会社の数が50社ある時は、1,125,899,906,842,623(約1126兆)パターンもあります。
これを火村氏が書いたコードのように、1社から50社までのパターンを構成すると、パターンの総数は2,251,799,813,685,196(約2252兆)通りとなります!これではソースコードがカオスなことになってしまいますね。

using System;
using System.Numerics;
class Program {
// 組み合わせ nCr を求めます。
static BigInteger Combinate( int n, int r ) {
// 中略
}
// nのk乗を求めます。
static BigInteger Pow( int n, int k ) {
// 中略
}
static void Main( string[] args ) {
// 1社から50社までのパターンの総和を求めます。
// ( Σ(Σ(nCi)) で求めた場合 )
BigInteger ans = 0;
for( int n = 1; n <= 50; n++ ) {
// n社ある時のパターンの数を求めます。
BigInteger sub = 0;
for( int i = 1; i <= n; i++ ) {
sub += Combinate( n, i );
}
ans += sub;
Console.WriteLine( $"{n}社ある時のパターンの数 = {sub} : Total = {ans}" );
}
Console.WriteLine();
// 1社から50社までのパターンの総和を求めます。
// ( 2^n - 1で求めた場合 )
ans = 0;
for( int n = 1; n <= 50; n++ ) {
// n社ある時のパターンの数を求めます。
BigInteger sub = Pow( 2, n ) - 1;
ans += sub;
Console.WriteLine( $"{n}社ある時のパターンの数 = {sub} : Total = {ans}" );
}
}
}[END]




コメント